Writing a CuTe DSL Kernel for NVFP4 GEMM
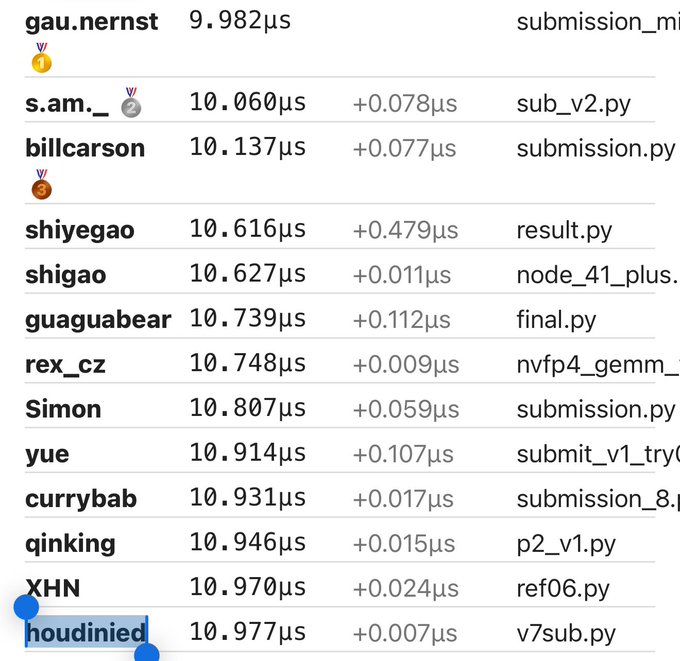
Hello world! This is my first blogpost of many, and it will be about my submission to GPU Mode's x NVIDIA Kernel Competition, specifically the NVFP4 General Matrix Multiplication (GEMM) challenge. I placed 13th, slightly less than 1 microsecond away from the winning submission.
The Challenge
Implement a block-scaled FP4 GEMM kernel that competes with NVIDIA's reference. The inputs:
- FP4 (Float4E2M1FN) matrices A and B
- FP8 (Float8E4M3FN) scale factors
- FP16 output C
- Blackwell SM100 with Tensor Memory (TMEM) and 5th-gen Tensor Cores
The benchmarks:
m=128, n=7168, k=16384
m=128, n=4096, k=7168
m=128, n=7168, k=2048All skinny matrices with small M. This regime needs careful tuning.
Block-Scaled FP4
Standard GEMM is C = A @ B. Block-scaled FP4 adds scale factors because 4 bits isn't enough precision on its own.
Values are grouped into blocks of 16, each with a scale factor:
C[i,j] = sum_k (A[i,k] * SFA[i,k//16]) * (B[j,k] * SFB[j,k//16])SFA and SFB undo the quantization per 16-element block. This is Microscaling (MX) format.
Blackwell Architecture
Tensor Memory (TMEM): 512-column scratchpad between registers and shared memory. Accumulators live here, so they don't compete with operands for register space.
5th-Gen Tensor Cores: Native block-scaled format support. Feed them FP4 + FP8 scale factors, they handle scaling internally. The tcgen05 instructions do this.
2-CTA Instructions: Two CTAs can fuse to work on a 256xN tile cooperatively. When M tile is 256, two CTAs pretend to be one.
Kernel Architecture
Warp-specialized persistent tile scheduler. 6 warps = 384 threads per CTA:
self.epilog_warp_id = (0, 1, 2, 3) # Warps 0-3: Epilogue (store results)
self.mma_warp_id = 4 # Warp 4: Matrix multiply
self.tma_warp_id = 5 # Warp 5: TMA loadsEach warp has one job:
- TMA Warp: Loads A, B, SFA, SFB from global to shared memory
- MMA Warp: Matrix multiply on tensor cores
- Epilogue Warps: Convert and store results to global memory
The Pipeline
Producer-consumer with multiple stages:
[TMA Loads] --> [SMEM Buffers] --> [MMA Compute] --> [TMEM Accum] --> [Epilogue Store]
^ | ^ | |
| ab_pipeline | acc_pipeline v
+------- (empty signal) ------------+ [GMEM]ab_pipeline manages shared memory buffers with barrier sync. TMA signals "full" when done loading, MMA signals "empty" when done consuming. Loads and compute overlap.
acc_pipeline manages the accumulator in tensor memory between MMA and epilogue.
Persistent Scheduling
Thread blocks stay resident and grab tiles until done:
tile_sched = utils.StaticPersistentTileScheduler.create(...)
work_tile = tile_sched.initial_work_tile_info()
while work_tile.is_valid_tile:
# Process current tile
tile_sched.advance_to_next_work()
work_tile = tile_sched.get_current_work()Amortizes launch overhead.
The Mainloop
MMA warp loops over K tiles:
for k_tile in cutlass.range(k_tile_cnt, unroll_full=True):
# Wait for A/B data in SMEM
ab_pipeline.consumer_wait(ab_consumer_state, peek_ab_full_status)
# Copy scale factors from SMEM to TMEM
cute.copy(tiled_copy_s2t_sfa, tCsSFA_compact_s2t_staged, tCtSFA_compact_s2t)
cute.copy(tiled_copy_s2t_sfb, tCsSFB_compact_s2t_staged, tCtSFB_compact_s2t)
# MMA for each K block
for kblock_idx in cutlass.range(num_kblocks, unroll_full=True):
tiled_mma.set(tcgen05.Field.SFA, tCtSFA[sf_kblock_coord].iterator)
tiled_mma.set(tcgen05.Field.SFB, tCtSFB_mma[sf_kblock_coord].iterator)
cute.gemm(tiled_mma, tCtAcc, tCrA[kblock_coord], tCrB[kblock_coord], tCtAcc)
tiled_mma.set(tcgen05.Field.ACCUMULATE, True)
# Done with this SMEM buffer
ab_pipeline.consumer_release(ab_consumer_state)cute.gemm invokes Blackwell tensor core instructions with block-scaled inputs.
Memory Layouts and TMA
Scale factors need a permuted layout for the tensor cores:
# ((Atom_M, Rest_M), (Atom_K, Rest_K), RestL)
sfa_layout = blockscaled_utils.tile_atom_to_shape_SF(a_tensor.shape, sf_vec_size)Multicast TMA broadcasts data to multiple CTAs:
if self.is_a_mcast:
a_full_mcast_mask = cpasync.create_tma_multicast_mask(
cluster_layout_vmnk, block_in_cluster_coord_vmnk, mcast_mode=2
)Same A slice goes to multiple CTAs computing different C columns.
Stage Calculation
How many pipeline stages fit in shared memory:
@staticmethod
def _compute_stages(...):
ab_bytes_per_stage = (
cute.size_in_bytes(a_dtype, a_smem_layout_stage_one)
+ cute.size_in_bytes(b_dtype, b_smem_layout_staged_one)
+ cute.size_in_bytes(sf_dtype, sfa_smem_layout_staged_one)
+ cute.size_in_bytes(sf_dtype, sfb_smem_layout_staged_one)
)
pos = (smem_capacity // occupancy - overhead) // ab_bytes_per_stage
num_ab_stage = max(pos, 5)More stages = more overlap = hidden memory latency. Blackwell has 228KB shared memory.
N=192 and N=64 Edge Cases
Special handling for tile sizes that don't divide evenly:
if cutlass.const_expr(self.cta_tile_shape_mnk[1] == 192):
offset = cutlass.Int32(2) if mma_tile_coord_mnl[1] % 2 == 1 else cutlass.Int32(0)
shifted_ptr = cute.recast_ptr(
acc_tmem_ptr + self.num_accumulator_tmem_cols + self.num_sfa_tmem_cols + offset,
dtype=self.sf_dtype,
)
tCtSFB_mma = cute.make_tensor(shifted_ptr, tCtSFB_layout)192 doesn't divide into tensor core tile sizes, so indexing gets creative.
The Epilogue
Convert FP32 accumulators to FP16 and store:
for subtile_idx in cutlass.range(subtile_cnt):
# Load accumulator from TMEM to registers
cute.copy(tiled_copy_t2r, tTR_tAcc_mn, tTR_rAcc)
# Convert to output type
acc_vec = tiled_copy_r2s.retile(tTR_rAcc).load()
acc_vec = epilogue_op(acc_vec.to(self.c_dtype))
tRS_rC.store(acc_vec)
# Store to SMEM
cute.copy(tiled_copy_r2s, tRS_rC, tRS_sC[(None, None, None, c_buffer)])
# TMA store to global memory
cute.copy(tma_atom_c, bSG_sC[(None, c_buffer)], bSG_gC[(None, real_subtile_idx)])Overlapping Accumulator
When N=256, only one accumulator stage fits in TMEM. Release it early:
if cutlass.const_expr(self.overlapping_accum):
if subtile_idx == self.iter_acc_early_release_in_epilogue:
cute.arch.fence_view_async_tmem_load()
acc_pipeline.consumer_release(acc_consumer_state)Epilogue releases the accumulator as soon as it's copied out, so MMA can start the next tile. Sub-tile double buffering.
Split-K (Correct but 7x Slower)
For k=16384, I tried split-K: multiple CTAs compute partial sums, then reduce.
Encoded split index into the L dimension:
SPLIT_K = 4
num_ctas_mnl_splitk = (num_ctas_m, num_ctas_n, l * split_k)
combined_l = cur_tile_coord[2]
actual_l = combined_l // split_k
split_idx = combined_l % split_k
k_tile_begin = split_idx * k_tile_cnt_per_split
k_tile_end = min((split_idx + 1) * k_tile_cnt_per_split, k_tile_cnt)Partial results go to FP32 workspace, then a Triton kernel reduces:
@triton.jit
def fused_reduce_kernel(
workspace_ptr, # (L*SPLIT_K, M, N) FP32
output_ptr, # (M, N, L) FP16
M, N, L, SPLIT_K: tl.constexpr,
BLOCK_SIZE: tl.constexpr = 256,
):
acc = tl.zeros([BLOCK_SIZE], dtype=tl.float32)
for s in range(SPLIT_K):
ws_offset = (l * SPLIT_K + s) * M * N + m * N + n
val = tl.load(workspace_ptr + ws_offset, mask=mask, other=0.0)
acc += valIt produces correct results. It's 7x slower.
Why:
- Workspace overhead: FP32 partials = 4x memory traffic vs direct FP16, plus extra kernel launch
- Reduction bottleneck: 4 non-coalesced global loads per output element
- Already saturated: N=7168 gives 56 output tiles. GPU is busy; split-K adds overhead
- Pipeline inefficiency: Fewer K-tiles per split = less work to hide latency
- Lost data reuse: Each split reloads A instead of reusing across K iterations
Split-K helps when M and N are small and you can't saturate the GPU. Here, N is big enough. The optimization wasn't needed.
What I Learned
CuTe is powerful but dense: Learning curve is steep. Reading CUTLASS source was essential.
Warp specialization enables overlap: Dedicated warps for loads/compute/store run truly in parallel.
Obvious isn't always fastest: Expected 256x256 tiles to win. 128x64 with more stages was better for skinny matrices.
TMEM changes everything: Accumulators in tensor memory don't compete with operands for registers.
Acknowledgements
Thanks to GPU Mode and NVIDIA for the competition. CUTLASS/CuTe docs and examples were invaluable.